箱线图介绍
箱形图是一张图表,能很好地指示数据中的值如何分布,尽管与直方图或密度图相比,箱线图似乎是原始的,但它们具有占用较少空间的优势,这在比较许多组或数据集之间的分布时非常有用。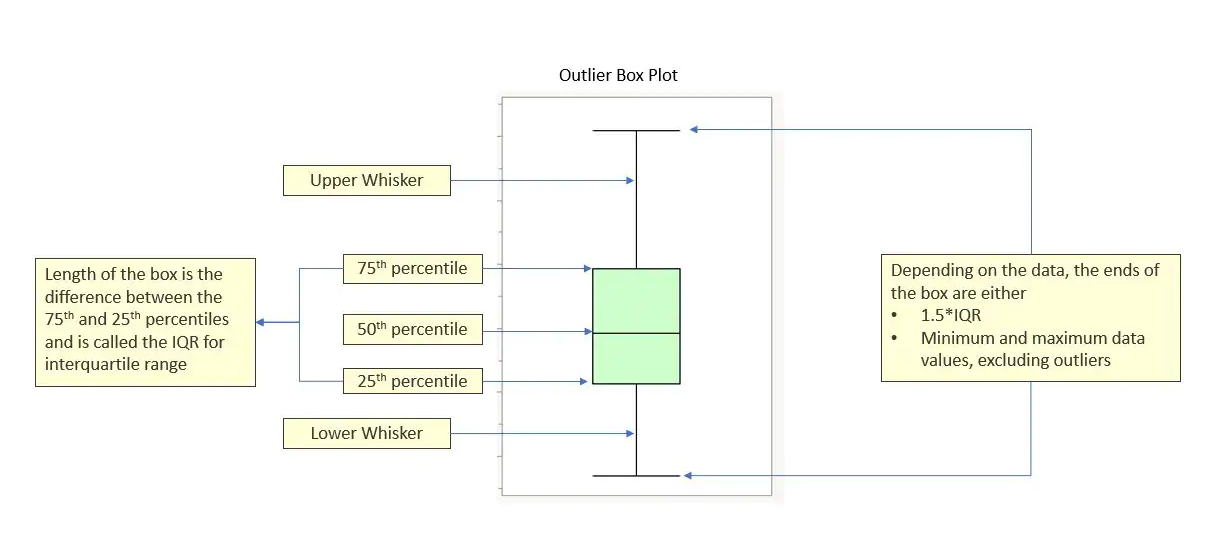
上图箱线图,箱线图是一个能够通过5个数字来描述数据的分布的标准方式,这5个数字包括:最小值,第一分位,中位数,第三分位数,最大值,箱线图能够明确的展示离群点的信息,同时能够让我们了解数据是否对称,数据如何分组、数据的峰度;
箱线图是一种基于五位数摘要(“最小”,第一四分位数(Q1),中位数,第三四分位数(Q3)和“最大”)显示数据分布的标准化方法。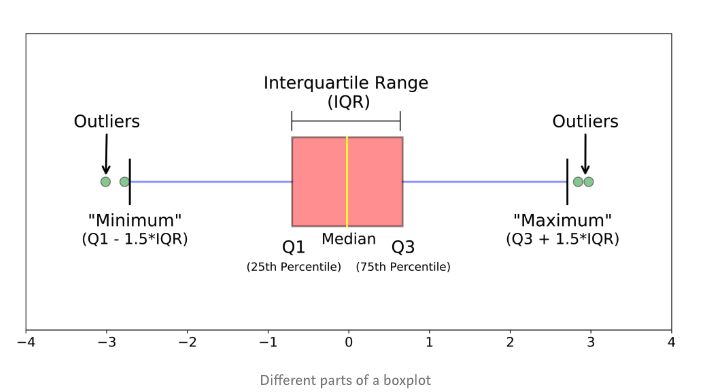
- 中位数(Q2 / 50th百分位数):数据集的中间值;
- 第一个四分位数(Q1 / 25百分位数):最小数(不是“最小值”)和数据集的中位数之间的中间数;
- 第三四分位数(Q3 / 75th Percentile):数据集的中位数和最大值之间的中间值(不是“最大值”);
- 四分位间距(IQR):第25至第75个百分点的距离;
- 晶须(蓝色显示)
- 离群值(显示为绿色圆圈)
- 最大值:Q3 + 1.5 * IQR 范围内的最大值(剔除异常值)
- 最小值:Q1 -1.5 * IQR 范围内的最小值(剔除异常值)
特殊注意点
如果会发现,箱线图中IQR相同,但是我们做箱线图时,图中的两条虚线(上下边缘到上下四分位的线)长度经常不同。
上下边缘的定义应该是上下四分位数加1.5IQR范围内数据的最大最小值,也就是说IQR并不是个定值,而是个取值范围。
1 | 举例[1,20,20,20,30,30,35],n=7,可以容易看出其各项参数: |
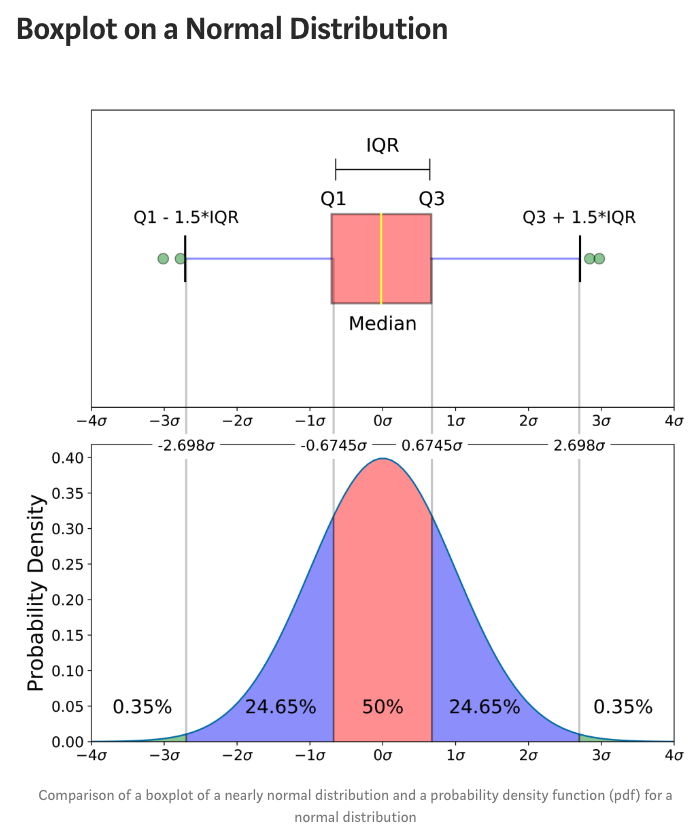
箱线图和概率密度图关系
对于一个近似正态数据,整天分布图和箱线图的概率分布关系如下图 ,