简述
- 1、如果两组数每组数的个数<30,且已知方差服从正态分布,可以比较2组数的均值是否显著不同,用 t检验;
- 2、如果两组数每组数的个数≥30,也可以比较2组数的均值是否显著不同,用 z检验;
- 3、如果两组数每组数的分布未知,可以比较2组数是否显著性同分布,可以用非参数检验 Mann-Whitney U test进行;
- 4、如果两组数已知都服从正态分布,可以比较2组数的方差是否显著相同,用F检验;
K-S检验
K-S检验(Kolmogorov-Smirnov检验),K-S检验不仅能够检验单个总体是否服从某一理论分布,还能够检验两总体分布是否存在显著差异。其原假设是:两组独立样本来自的两总体的分布无显著差异。
K-S检验以变量的秩作为分析对象,检验两个独立样本群体,或者一个样本群体和一个特定标准分布之间的关系。K-S就是对两组数据的累积分布进行比较,寻找两个群体累积分布曲线之前的最大值作为D值。获得D值后,查表确定临界值。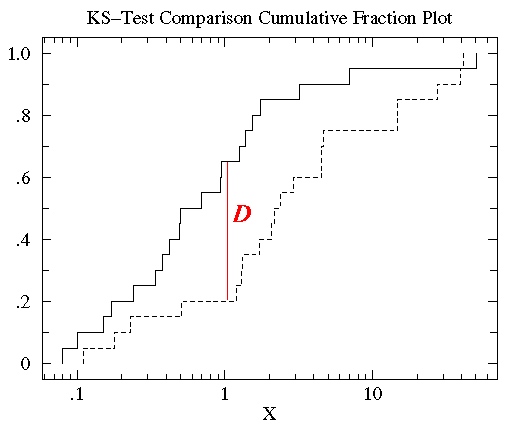
Z-test
Z-Test: Definition, Uses in Statistics, and Example
z分数是一种统计度量,用于量化数据点与数据集平均值之间的单位距离(距离单位是总体的标准差)。它以标准差的形式表示。它指示数据点与分布平均值之间距离由几个标准差。如果 Z 分数为 0,则表示数据点的分数与平均分数相同。 Z 分数为 1.0 表示与平均值相差一个标准差的值。 Z 分数可以是正数或负数,正值表示分数高于平均值,负值表示分数低于平均值。
z 检验是一种统计检验,用于在方差已知且样本量较大时确定两个大致符合正态分布的总体均值(大致符合正态分布,否则测试不起作用)是否不同。它还可用于将一个平均值与假设值进行比较。
z 检验最适用于大于 30 个样本,因为根据中心极限定理,随着样本数量变大,样本被认为近似正态分布。
进行 z 检验时,应说明原假设和备择假设以及 alpha 水平。应计算z 分数,也称为检验统计量,并说明结果和结论。 z 统计量或 z 分数是一个数字,表示从 z 检验得出的分数高于或低于总体平均数的标准差有多少。
计算方式如下:
$$ z = ( x - μ ) / \sqrt{\frac{σ^2}{n}} $$
z = Z-score
x = 待评估数据的均值
n = 待评估数据的样本个数
μ = 均值
σ = 标准差 ; σ^2 = 方差
当我们待测数据是单一数值时,对应的计算公式可以简化为:
$$ z = ( x - μ ) / σ $$
Z-score 对应概率值表
T-test
t 检验比较两个数据集的平均值并确定它们是否来自同一总体。例如,物理课学生的成绩和写作课不同组学生的成绩不太可能具有相同的平均值和标准差。同样,从药物测试的安慰剂喂养对照组中采集的样本和从药物处方组中采集的样本应该具有稍微不同的平均值和标准差。
T 检验的场景:
- 药效测试时,按照标准程序,将药物给予一组患者,并向另一组(称为对照组)给予安慰剂。t 检验可用于确定结果是否显着且适用于整个人群,或者它们是否是随机的且不是由于药物干预所致。
t 检验时做出四个假设: - 收集的数据必须遵循连续或顺序尺度,例如智商测试的分数。
计算方式如下:
- 计算配对t检验
计算配对 t 检验的 t 值和自由度的公式为:
$$T=\frac{mean1−mean2}{\frac{s(diff)}{\sqrt{n}}}$$
其中:
mean1 and mean2= 两个数据集的均值
s(diff)=配对数据的差值的标准差
n=样本集合大小(配对数据的数目)
n−1=自由度