前面的介绍,我们遇到过两种类型的数据:表格数据和图像数据。 对于图像数据,我们设计了专门的卷积神经网络架构来为这类特殊的数据结构建模。我们在处理这俩各种类型时,这两类数据本身是无序的(顺序不会影响对数据的理解)。
最重要的是,到目前为止我们默认数据都来自于某种分布,并且所有样本都是独立同分布的 (independently and identically distributed,i.i.d.)每次我门处理一个独立数据,数据间是无关的。然而,大多数的数据并非如此,很多元素都是相互连接的,例如,文章中的单词是按顺序写的,如果顺序被随机地重排,就很难理解文章原始的意思。视频中的图像帧、对话中的音频信号以及网站上的浏览行为,股票的变化,都是有顺序的。一个人说了:我喜欢旅游,其中最喜欢的地方是云南,以后有机会一定要去__.这里填空,人应该都知道是填“云南“。因为我们是根据上下文的内容推断出来的,但机器要做到这一步就相当得难了。因此,就有了现在的循环神经网络,他的本质是:像人一样拥有记忆的能力。因此,他的输出就依赖于当前的输入和记忆。
另一个问题来自这样一个事实: 我们不仅仅可以接收一个序列作为输入,而是还可能期望继续猜测这个序列的后续。 例如,一个任务可以是继续预测$2,4,6,8,10…$。 这在时间序列分析中是相当常见的,可以用来预测股市的波动、 患者的体温曲线或者赛车所需的加速度。 同理,我们需要能够处理这些数据的特定模型。
如果说卷积神经网络可以有效地处理空间信息,那么我们这里要介绍的 循环神经网络(recurrent neural network,RNN) 则可以更好的处理序列信息。循环神经网络通过引入状态变量存储过去的信息(记忆)和当前的输入,从而可以确定当前的输出。
RNN的网络结构及原理
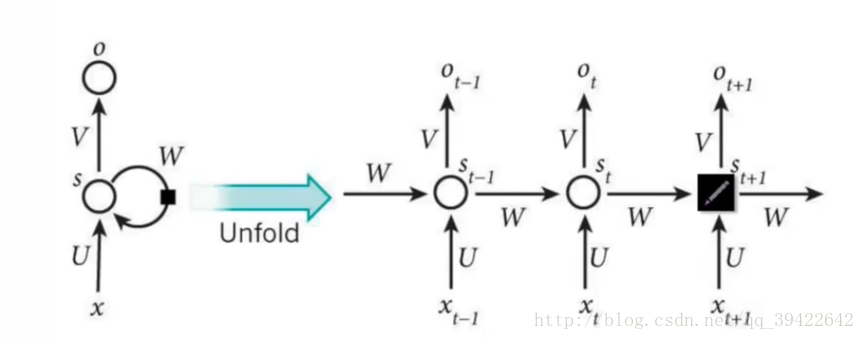
RNN的网络结构如下:
其中每个圆圈可以看作是一个单元,而且每个单元做的事情也是一样的,因此可以折叠呈左半图的样子。用一句话解释RNN,就是一个单元结构重复使用。
RNN是一个序列到序列的模型,假设$x_{t−1},x_t,x_{t+1}$是一个输入:“我是中国“,那么$o_{t−1},o_t$就应该对应”是”,”中国”这两个,预测下一个词最有可能是什么?就是$o_{t+1}$应该是”人”的概率比较大。
因此,我们可以做这样的定义:
$X_t$:表示t时刻的输入,$o_t$:表示t时刻的输出,$S_t$:表示t时刻的记忆
可以看到和之前的卷积或其他网络的主要区别是,在生成输出时,我们引入记忆 $S_t$ 的信息。输出结果是由记忆和输入共同决定的。而随着我们每处理一个问题,可能我们会更新记忆(学习到新知识)。RNN在这点上也类似,神经网络最擅长做的就是通过一系列参数把很多内容整合到一起,然后学习这个参数,因此就定义了RNN的基础:
$S_t=f(U∗X_t+W∗S_{t−1})$
可以看到,我们每个时间点的记忆由上一个时间点的记忆,和当前时间点接收到的信息共同构成。大家可能会很好奇,为什么还要加一个 $f()$ 函数,其实这个函数是神经网络中的激活函数,但为什么要加上它呢?
举个例子,假如你在大学学了非常好的解题方法,那你初中那时候的解题方法还要用吗?显然是不用了的。RNN的想法也一样,既然我能记忆了,那我当然是只记重要的信息啦,其他不重要的,就肯定会忘记,是吧。但是在神经网络中什么最适合过滤信息呀?肯定是激活函数嘛,因此在这里就套用一个激活函数,来做一个非线性映射,来过滤信息,这个激活函数可能为tanh,也可为其他。
在每个时间点t,我们基于上述方式获得了$S_t$ (整合了t时刻的输入和之前的记忆),下一步就是预测t时刻的输出 $o_t$。运用softmax来预测每个词出现的概率再合适不过了,但预测不能直接带用一个矩阵来预测呀,所有预测的时候还要带一个权重矩阵V,用公式表示为:
$o_t=softmax(V S_t)$
RNN中的结构细节:
- 可以把$S_t$当作隐状态,捕捉了之前时间点上的信息。就像你去考研一样,考的时候记住了你能记住的所有信息。
- $o_t$是由当前时间以及之前所有的记忆得到的。就是你考研之后做的考试卷子,是用你的记忆得到的。
- 很可惜的是,$S_t$并不能捕捉之前所有时间点的信息。就像你考研不能记住所有的英语单词一样。
- 和卷积神经网络一样,这里的网络中每个cell都共享了一组参数(U,V,W),这样就能极大的降低计算量了。
- $o_t$在很多情况下都是不存在的,因为很多任务,比如文本情感分析,都是只关注最后的结果的。就像考研之后选择学校,学校不会管你到底怎么努力,怎么心酸的准备考研,而只关注你最后考了多少分。
RNN的改进: 双向RNN
在有些情况,比如有一部电视剧,在第三集的时候才出现的人物,现在让预测一下在第三集中出现的人物名字,你用前面两集的内容是预测不出来的,所以你需要用到第四,第五集的内容来预测第三集的内容,这就是双向RNN的想法。如图是双向RNN的图解:
从前往后:$\overrightarrow{S_t}=f(\overrightarrow{U}∗X_t+\overrightarrow{W}∗S_{t−1}+\overrightarrow{b})$
从后往前:$\overleftarrow{S_t}=f(\overleftarrow{U}∗X_t+\overleftarrow{W}∗S_{t+1}+\overleftarrow{b})$
输出:$o_t=softmax(V∗[\overrightarrow{S_t};\overleftarrow{S_t}])$
这里的 $[\overrightarrow{S_t};\overleftarrow{S_t}]$做的是一个拼接,如果他们都是1000 x 1维的,拼接在一起就是1000 x 2维的了。
双向RNN需要的内存是单向RNN的两倍,因为在同一时间点,双向RNN需要保存两个方向上的权重参数,在分类的时候,需要同时输入两个隐藏层输出的信息。
RNN的改进2:深层双向RNN

深层的双向RNN(Stacked Bidirectional RNN)的结构如上图所示。上图是一个堆叠了3个隐藏层的RNN网络。
和之前的区别就是这时,我们的forward和backwards的矩阵计算时递归(递归处理不同的层)
从前往后:$\overrightarrow{S_t^l}=f(\overrightarrow{U^l}∗S^{l-1}t+\overrightarrow{W^l}∗S^l{t−1}+\overrightarrow{b^l})$
从后往前:$\overleftarrow{S^l_t}=f(\overleftarrow{U^l}∗S^{l-1}t+\overleftarrow{W^l}∗S{t+1}+\overleftarrow{b^l})$
输出:$o_t=softmax(V∗[\overrightarrow{S_t^l};\overleftarrow{S^l_t}])$
这个时候,每个隐藏层的每个节点在计算是,依然是需要两个输入,比如我们计算 $S^l_{t}$ (l对应隐藏层的索引、t对应时间点)时,第一个输入就是同一隐藏层前一时刻传递过来的信息$S^l_{t−1}$,和同一时刻上一隐藏层传过来的信息$S^{l-1}_t=[\overrightarrow{S_t^{l-1}};\overleftarrow{S^{l-1}_t}]$,包括前向和后向的
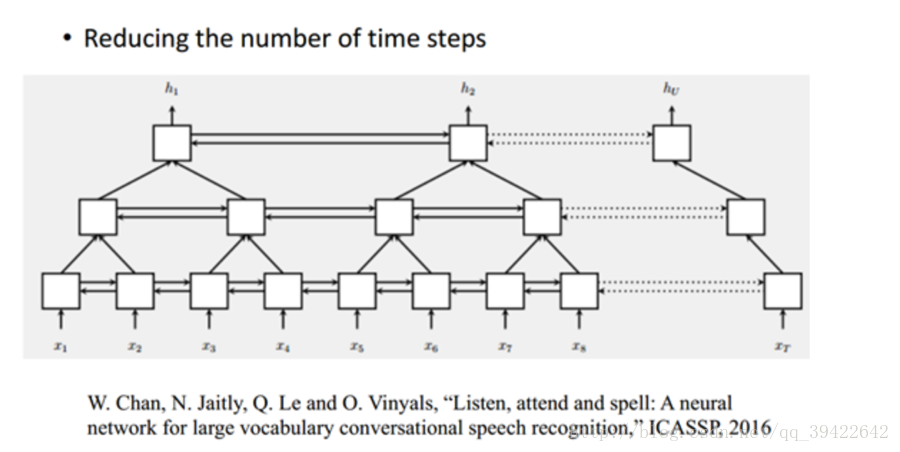
Pyramidal RNN 金字塔RNN
上图是谷歌的W.Chan做的一个测试,它原先要做的是语音识别,他要用序列到序列的模型做语音识别,序列到序列就是说,输入一个序列然后就输出一个序列。
由图我们发现,上一层的两个输出,作为当前层的输入,如果是非常长的序列的话,这样做的话,每一层的序列都比上一层短(示例时上一层的一半长度),但当前层的输入 $f(x)$也会随之增多,貌似看一起相互抵消,运算量并没有什么改进。
但我们知道,对于一层来说,它是从前往后递归的,比如要预测一个股市的变化,数据必须先预测昨天,再预测今天,最后预测明天,也即是说预测必须具有连续性。
但每一层的$f$运算是可以并行的,从这个角度来看,运算量还是可以接受的,特别是在原始输入序列较短的时候还是有优势的。
模型的训练
通过前面的介绍,我们可以知道,所有的RNN,都可以抽象成如下的两个部分:
第一步,结合当前时间点的输入和上一时间点的记忆,生成当前时间点的记忆(如果时双向神经网络会有来自两个方向的记忆):
- 从前往后:$\overrightarrow{S_t^l}=f(\overrightarrow{U^l}∗S^{l-1}t+\overrightarrow{W^l}∗S^l{t−1}+\overrightarrow{b^l})$
- 从后往前:$\overleftarrow{S^l_t}=f(\overleftarrow{U^l}∗S^{l-1}t+\overleftarrow{W^l}∗S{t+1}+\overleftarrow{b^l})$
第二部,基于当前时间点的记忆生成当前时间点的输出(类频率、或频率)
输出:$o_t=softmax(V∗[\overrightarrow{S_t^l};\overleftarrow{S^l_t}])$
所以完成了模型框架后,我们要应用模型,其实要解决的就是寻找最优参数($U、W、V$)。
为了找到最好的参数,我们首先要构建一个评估参数好坏的指标,和之前的模型一样,一般采用损失函数。
损失函数
t时刻的损失:$E_t(y_t,y_t)=−y_t\log{\hat{y}_t}$
其中 $y_t$是t时刻的标准答案,是一个只有一个维度是1,其他都是0的向量; $y^t$是我们预测出来的结果,与 $yt$ 的维度一样,但它是一个概率向量,里面是每个词出现的概率。因为对结果的影响,肯定不止一个时刻,因此需要把所有时刻的造成的损失都加起来:
$$E(y_t,\hat{y}_t)=\sum_t{E_t(y_t,\hat{y}t)}=−\sum{t}{y_tlog\hat{y_t}}$$
获得随时函数后,我们就可以根据损失函数求解最优参数了。再RNN中计算最优解,用的是BPTT。
序列模型应用
输入或者输出中包含有序列数据的模型叫做序列模型。典型应用比如:
- 语音识别: 输入输出都为序列。
- 音乐生成: 输出为序列。
- 情感分析:输入为序列。
- DNA序列分析:输入为序列。
- 机器翻译:输入输出都为序列。
- 视频行为识别:输入为序列。
- 命名实体识别:输入输出都为序列。
统计工具
要处理序列数据,我们需要统计工具和新的神经网络架构。为了便于后续的理解,我们以 下图所示(富士100指数)股票价格为例。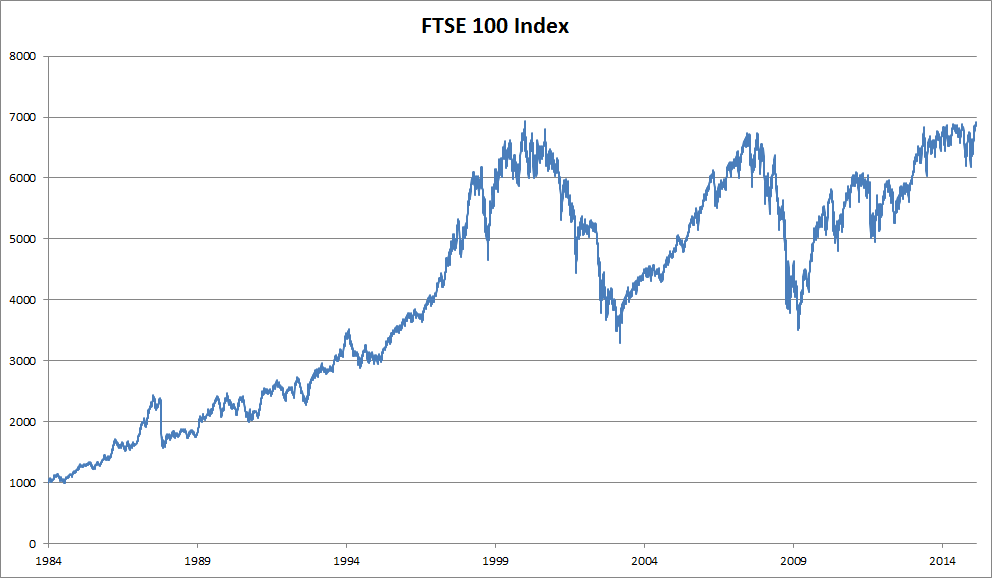
其中,用 $x_t$ 表示价格,即在时间步(time step)$t \in{Z^+}$ 时,观察到的价格。 请注意,$t$对于本文中的序列通常是离散的,并在整数或其子集上变化。 假设一个交易员想在$t$日的股市中表现良好,于是通过以下途径预测:
$x_t \sim P(x_t|x_{t-1},…,x_1)$
自回归模型
为了实现这个预测,可以使用回归模型,我们需要解决的只有一个主要问题:输入数据的数量, 输入 $x_{t-1},…,x_1$ 本身因$t$而异。 也就是说,输入数据的数量这个数字将会随着我们遇到的数据量的增加而增加, 因此需要一个近似方法来使这个计算变得容易处理。 本章后面的大部分内容将围绕着如何有效估计 $P(x_t|x_{t-1},…,x_1)$ 展开。 简单地说,它归结为以下两种策略。
在现实情况下相当长的序列 $x_{t-1},…,x_1$ 可能是不必要的, 因此我们只需要满足某个长度为的时间跨度 $\tau$, 即使用观测序列 $x_{t-1},…,x_{t-\tau}$。最直接的好处就是在我们的历史数据达到 $\tau$ 后,参数的数量总是不变的,从而让我们具备训练一个神经网络的基础。因为这种模型是对自己执行回归,所以这种模型被称为自回归模型。
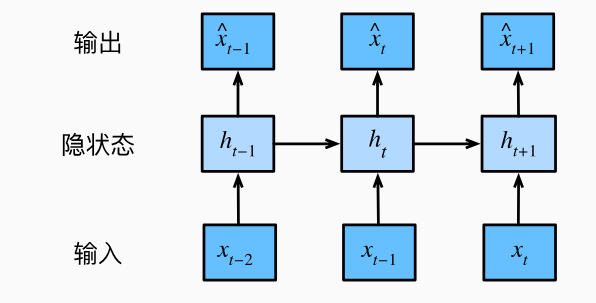
还有一种方案是如下图所示,总是保留一些对过去观测的总结 $h_{t}$,并且同时更新预测结果 $\hat{x}t$ 和总结 $h{t}$。这就形成了,基于 $\hat{x}_t = P(x_t|h_{t})$ 估计 $x_t$ , 以及 $h_t = g(h_{t-1}|x_{t-1})$ 更新的模型。由于总结 $h_t$ 是从未被观测到的,所以这类模型也被成为 隐变量自回归模型。
执行案例
文本处理
预处理
- 将文本作为字符串加载到内存中。
- 将字符串拆分为词元(如单词和字符)。
- 建立一个词表,将拆分的词元映射到数字索引。
- 将文本转换为数字索引序列,方便模型操作。